The Babylonian method to solve quadratic equations

TLDR;

Quadratic equations are a ubiquitous part of our daily lives, often subtly present in the form of parabolas. Whether we're aware of it or not, these mathematical expressions shape much of the world around us -- from the arcs of thrown balls to the curves of satellite dishes.

Around 4000 years ago, circa 2000 B.C., the Babylonians discovered a geometric method to solve quadratic equations. This post celebrates the ingenuity and straightforwardness of their approach.

Bouncing ball	Satellite dish
Sydney harbor bridge	Water trajectory

Babylonians, who lived in the fertile region between Euphrates River and Tigris River were also interested in quadratic equations.

Consider this cute puzzle from 2000 B.C.

I have added the area and two-thirds of [ the side of ] my square and it is 35. What is the side of my square?

In modern notation, this puzzle corresponds to solving for $x$ in the following equation. $$x^2 + \frac{2x}{3} = 35$$

Babylonians had a geometric way of solving such equations. Let me explain. To solve a general quadratic equations of the form

\begin{equation} \label{eq:xpq} x^2 + px = q \end{equation}

Babylonians considered the following square.

A square with each side $x + \frac{p}{2}$ divided into four individual blocks.

The area of the larger square with side length $x + \frac{p}{2}$ is the sum of the areas of the individual squares and rectangles shaded in various colors above. Therefore, \begin{align} (x + \frac{p}{2}) ^2 & = x^2 + 2 \frac{p}{2} x + \frac{p^2}{4} \nonumber \\ &= x^2 + px + \frac{p^2}{4} \label{eq:test} \nonumber \\ & = q + \frac{p^2}{4} &\text{[using equality \eqref{eq:xpq}]} \end{align}

Therefore, \begin{align*} x = \sqrt{q + \frac{p^2}{4}} - \frac{p}{2} \end{align*}

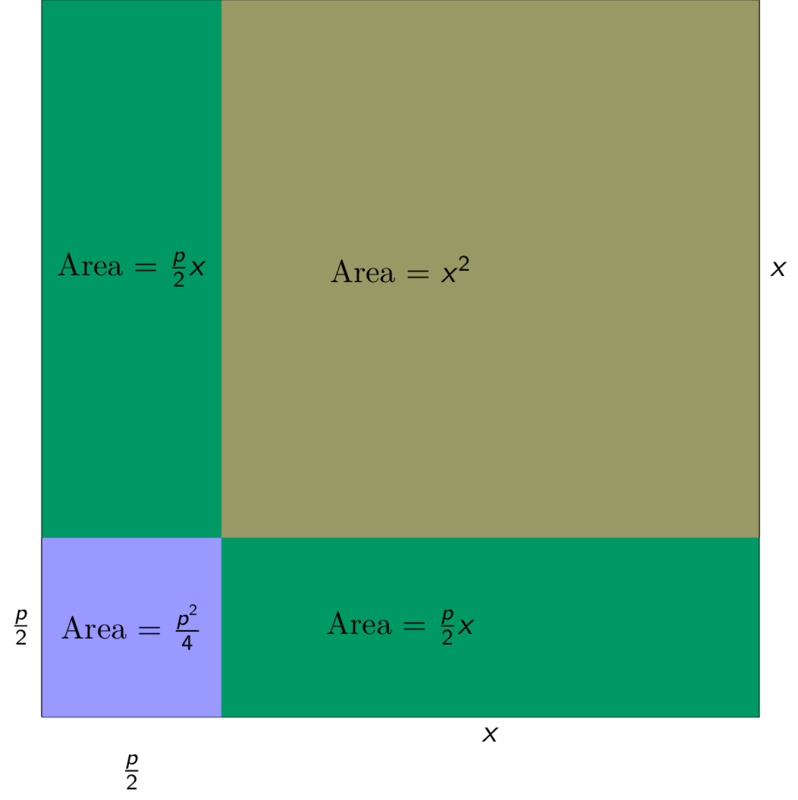
QED 😀

Here is a trivia if you enjoyed reading this far.

Why did the Babylonians represent a general quadratic equation in the form $$x^2 + px = q$$ as opposed to the contemporary form $$ax^2 + bx + c = 0$$